Question

51, 48, 45, 43,... write a rule for the nth term of the sequence then find a20 base

Answer 1

general rule

an = 51 - 3 (n - 1)

a20 = -6

Step-by-step explanation:

Looking at the first four terms of the series we see that each consecutive term is 3 less than the previous term. For example. 51 - 3 = 48, 48 - 3 = 45 and so on.

Therefore the general rule for the nth term is

`a_n=51-3(n-1)`

note that the use of using n - 1 is that when n = 1 we have

a_1 = 51 - 3(1-1) = 51 - 0 = 51

in other words, n - 1 helps us in setting a1 = 51.

Now once we have the general rule, we now find a20

`a_(20)=51-3(20-1)`

which simplifies to give

`a_(20)=51-3\cdot19`
`\therefore a_(20)=-6`

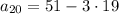
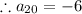
which is our answer!