Question

I'm trying to figure out the solve this quadratic function and I had a tutor helping me but my phone lost connection and I only made it halfway through this is the problem I will take a picture

Answer 1

Given a function as shown below:

`P(x)=550x-1240-2x^2`
`\begin{gathered} for\text{ profit maximization } \\ P(x)=550x-1240-2x^2 \\ (dp(x))/(dx)=550-4x \\ 0\text{ = 550 -4x} \\ 4x\text{ = 550} \\ x=\text{ }(550)/(4) \\ x=137.5 \\ x=\text{ 138 (nearest whole number)} \end{gathered}`

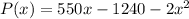
Hence to maximize the profit at least 138 items must be sold

And the maximum profit that can be earned is derived by substituting 138 it to p(x)

`\begin{gathered} P(x)=550x-1240-2x^2 \\ P(x)=550(138)-1240-2(138)^2 \\ P(x)=\text{ 36572}.00 \end{gathered}`

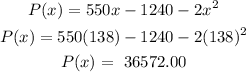
Hence the maximum profit is $36572.00

The minimum item that must be sold to make a profit can be found by solving the following quadratic inequality:

`P(x)=550x-1240-2x^2\ge0`

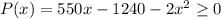
And the solution is given as

`\begin{gathered} (-√(73145)+275)/(2)\le\: x\le(√(73145)+275)/(2) \\ 2.27333\le\: x\le\: 272.72666 \end{gathered}`

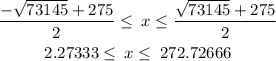
Hence, the company must sell a minimum of 3 items to make a profit