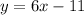Question

The math is “Equation of a line given two points” I wrote the question and answered it but I’m not sure if I got it right or even did the steps correctly please help

Answer 1

The equation of a line with slope m and y-intercept b in slope-intercept form is:

`y=mx+b`

Use the slope formula to find the slope of the line that passes through two points:

`m=(y_2-y_1)/(x_2-x_1)`

Replace the coordinates of the points (3,7) and (2,1):

`m=(7-1)/(3-2)=(6)/(1)=6`

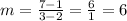
Replace the value of m into the equation of the line in slope-intercept form:

`y=6x+b`

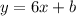
To find the y-intercept, replace the coordinates of any of the given points and solve for b. For instance, use x=2 and y=1:

`\begin{gathered} 1=6(2)+b \\ \Rightarrow1=12+b \\ \Rightarrow1-12=b \\ \therefore b=-11 \end{gathered}`

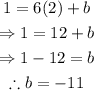
Therefore, the equation of the line that passes through the points (2,1) and (3,7) in slope-intercept form, is:

`y=6x-11`