Given the information on the coordinate plane, we can see that the points A and B are (-2,-2) and (2,-2) respectively. Then, to find the slope we have:
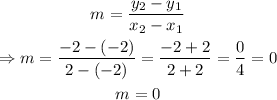
We have that the slope is 0, and to find the equation, we can use the equation y=mx+b to find out, using either points A or B:
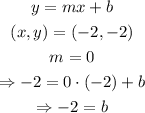
Therefore, the equation of the diagonal AB is y=-2