1 Answer

Sebastian Hojas · Answer 1 · 2023-12-08T15:21:34+0000

Given the triangle shown in the exercise, you know that it is a Right Triangle. This means that it has an angle that measures 90 degrees.

• By definition, the sum of the interior angles of a triangle is 180 degrees. Then, knowing this, you can set up the following equation:

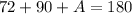
$72\degree+90\degree+A=180\degree$

Then, solving for "A", you get:

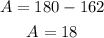
$\begin{gathered} A=180\degree-162\degree \\ A=18\degree \end{gathered}$

• To find the length "a", you can use this Trigonometric Function:

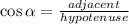
$\cos \alpha=(adjacent)/(hypotenuse)$

In this case:

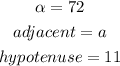
$\begin{gathered} \alpha=72\degree \\ adjacent=a \\ hypotenuse=11 \end{gathered}$

Then, substituting values and solving for "a", you get:

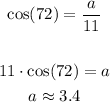
$\begin{gathered} \cos (72\degree)=(a)/(11) \\ \\ 11\cdot\cos (72\degree)=a \\ a\approx3.4 \end{gathered}$

• To find the length "b", you can use this Trigonometric Function:

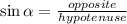
$\sin \alpha=(opposite)/(hypotenuse)$

Since:

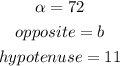
$\begin{gathered} \alpha=72\degree \\ opposite=b \\ hypotenuse=11 \end{gathered}$

You can substitute values and solve for "b":

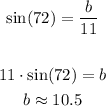
$\begin{gathered} \sin (72\degree)=(b)/(11) \\ \\ 11\cdot\sin (72\degree)=b \\ b\approx10.5 \end{gathered}$

Therefore, the answer is: Last option.

Please log in or register to add a comment.