A polynomial is an algebraic expression of ordered addition, subtraction, and multiplication of variables, constants, and exponents. A polynomial can have more than one variable (x, y, z), constants (integers or fractions), and exponents (which can only be positive integers).
Then, let us see examples of what a polynomial is and is not:
• They are not polynomials
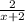
Because the variable cannot be in the denominator
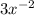
Because the exponent is -2 and the exponents can only be 0,1,2, ..., etc.
![\sqrt[]{x}=x^{(1)/(2)}](https://img.qammunity.org/2023/formulas/mathematics/college/qs7vpqo09ne5jtgklc0yiwbw2nxtgclx0u.png)
Because the exponent cannot be a fraction
• They are polynomials
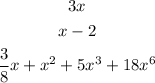
According to the above, the given expression is a polynomial because it is a sum of a variable with integer and positive exponents. Also, the variable is not in the denominator of any fraction.
• Now, according to the ,number of terms, in a polynomial, there are ,3 types of polynomials,. They are ,monomial, binomial and trinomial,. For example:
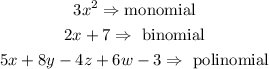
In this case, the given expression has two terms, and then it is a binomial.
Finally, the degree of a polynomial is the highest exponent value of any of its terms.
Therefore, the degree of the given polynomial is 4.