Question

The function f(x) = x^2 - 3x + 21 models the area of a rectangle with a side length of x inches. The function g(x) = 2x^2 + 2x + 7 models the area of a second rectangle with the same side length. Which function, h(x), can be used to determine how much larger the second rectangle is than the first rectangle?

Answer 1

we are given the areas of two rectangles modeled as two functions. Two determine how much large one rectangle is from the other we will subtract the functions for the areas, like this:

`g(x)-f(x)`

Replacing the values we get:

`2x^2+2x+7-(x^2-3x+21)`

Now we change the sign of the expression inside the parenthesis:

`2x^2+2x+7-x^2+3x-21`

Now we associate like terms:

`(2x^2-x^2)+(2x+3x)+(7-21)`

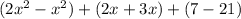
adding like terms:

`x^2+5x-14`

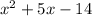
And thus we get the function.