Question

Solve the quadratic by completing the square.x^2 + 14x = -69

Answer 1

We have to solve this equation by completing the square.

We have two terms from the quadratic equation: x² + 14x, so we can add the third term as:

`\begin{gathered} x^2+14x=-69 \\ x^2+2(7)x+7^2=-69+7^2 \end{gathered}`

We add the same term to both sides of the equation to preserve the equality.

We now can continue solving the equation as:

`\begin{gathered} x^2+2(7)x+49=-69+49 \\ (x+7)^2=-20 \\ x+7=\pm√(-20) \\ x=-7\pm√(-20) \end{gathered}`

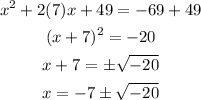
This equation does not have solutions for x for the set of real values, as we have a square root of a negative number.

We can express the solution as complex numbers as:

`\begin{gathered} x=-7\pm√(-20) \\ x=-7\pm√(20)i \\ x=-7\pm2√(5)i \end{gathered}`

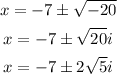
Answer: the solutions for the equation are x = -7 - 2(√5)i and x = -7 + 2(√5)i.