Given:
Mass (m) = 56 kg
Potential Energy (PE) = 46000000 Joules
Let's find the height the meteor enters our atmosphere.
To find the height, apply the Potential Energy formula below:
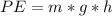
Since we are to find the height(h), rewrite the equation for h:
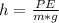
Where:
g is the acceleration due to gravity = 9.8 m/s^2
Input values into the equation:
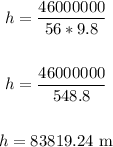
Therefore, the height it enters our atmosphere is 83819.24 meters
ANSWER:
83819.2 m