Question

10) A drug causes side effects for 18% of patients. If the drug is given to 230 patients, find the probability that the number ofpatients who experience side effects isa)exactly 35b) less than 30c) between 37 and 45 inclusived)more than 5011) Let the random variable X represent the number of patients who experience side effects in problem #10.a)Compute the mean, variance, and standard deviation of X.b) Interpret the mean.C)Would it be unusual if 32 patients experienced side effects? (explain why or why not)

Answer 1

a)

The drug causes side effects for 18% of patients, that is, every patient who was exposed to the drug has p = 18% chance of have side effects.

If X represent the number of patients who experience side effects betwen n = 230 observed, and considering a binomial distribution, we have:

`\begin{gathered} Mean(X)=n\cdot p \\ Mean(X)=230\cdot0.18 \\ Mean(X)=41.4 \end{gathered}`

Since or data set only deals with whole numbers, we can approximate the mean to 41

The variance is given by:

`\begin{gathered} Var(X)=n\cdot p\cdot(1-p) \\ Var(X)=230\cdot0.18\cdot(1-0.18) \\ Var(X)=33.9\approx40 \end{gathered}`

Then, the standard deviation of X is:

`\begin{gathered} \sigma=√(Var(X)) \\ \sigma=√(50) \\ \sigma\approx6 \end{gathered}`

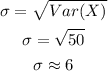
b)

The mean is the expected value of a variable. That is, most probable value to be identified,

c)

Since the 95% tolerance range is between 29 and 53, is would be usual if 32 patients experience side effects