Question

Solve the system by substitution.5x - 2y + 3z =62x - 4y - 3z = - 23X + 6y - 8z = 1X =Y =Z =

Answer 1

X=1

Y=4

Z=3

Step-by-step explanation

`\begin{gathered} 5x-2y+3z=6\Rightarrow equation(1) \\ 2x-4y-3z=-23\Rightarrow equation(1) \\ x+6y-8z=1\Rightarrow equation(1) \end{gathered}`

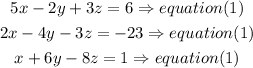
Step 1

b) isolate the x variable in equaiton (1) and equation(2)

so

`\begin{gathered} 5x-2y+3z=6\Rightarrow equation(1) \\ \text{add 2y in both sides} \\ 5x-2y+3z+2y=6+2y \\ 5x+3z=6+2y \\ \text{subtract 3z in both sides} \\ 5x+3z-3z=6+2y-3z \\ 5x=6+2y-3z \\ \text{divide both sides by 5} \\ (5x)/(5)=(6+2y-3z)/(5) \\ x=(6+2y-3z)/(5)\Rightarrow equation(1A) \end{gathered}`

and

`\begin{gathered} 2x-4y-3z=-23\Rightarrow equation(2) \\ 2x=-23+4y+3z \\ x=(-23+4y+3z)/(2) \end{gathered}`

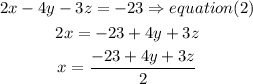
b) now replace x value from equaton (1) into equation (3)

`\begin{gathered} x+6y-8z=1 \\ (6+2y-3z)/(5)+6y-8z=1 \\ (6+2y-3z)/(5)=1-6y+8z \\ 6+2y-3z=5(1-6y+8z) \\ 6+2y-3z=5-30y+40z \\ 6-5+2y+30y-3z-40z=0 \\ 1+32y-43z=0 \\ 32y-43z=-1\Rightarrow equation(4) \end{gathered}`

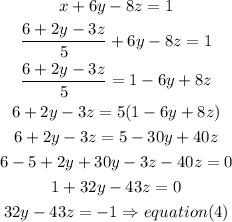
c) now replace x value from equaton (2) into equation (3)

`\begin{gathered} x+6y-8z=1 \\ (-23+4y+3z)/(2)+6y-8z=1 \\ (-23+4y+3z)/(2)=1-6y+8z \\ -23+4y+3z=2(1-6y+8z) \\ -23+4y+3z=2-12y+16z \\ -23+4y+3z-2+12y-16z=0 \\ -25+16y-13z=0 \\ 16y-13z=25\Rightarrow equation(5) \end{gathered}`

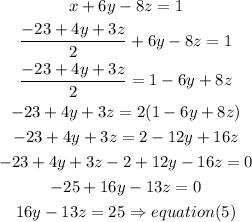
Step 2

now, use equation (4) and equation(5) to

`\begin{gathered} 32y-43z=-1\Rightarrow equation(4) \\ 16y-13z=25\Rightarrow equation(5) \end{gathered}`

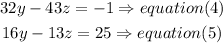
a) isolate the y value from equation(1) and substitute into equation(2)

z=

`\begin{gathered} 32y-43z=-1\Rightarrow equation(4) \\ 32y=-1+43z \\ y=(-1+43z)/(32) \\ \text{replace in eq(5)} \\ 16y-13z=25\Rightarrow equation(5) \\ 16((-1+43z)/(32))-13z=25 \\ ((-1+43z)/(2))-13z=25 \\ ((-1+43z)/(2))=25+13z \\ -1+43z=2(25+13z) \\ -1+43z=50+26z \\ 43z-26z=50+1 \\ 17z=51 \\ z=(51)/(17) \\ z=3 \end{gathered}`

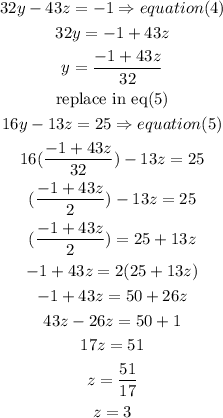
so

Z= 3

b) replace the z value in equation (4) to find z

`\begin{gathered} 32y-43z=-1\Rightarrow equation(4) \\ 32y-43(3)=-1 \\ 32y=-1+129 \\ 32y=128 \\ y=4 \\ \end{gathered}`

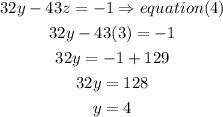
Y=4

c) finally,l replace the Z and Y value in equation (1A)

`\begin{gathered} x=(6+2y-3z)/(5)\Rightarrow equation(1A) \\ x=(6+2(4)-3(3))/(5) \\ x=(6+8-9)/(5)=(5)/(5)=1 \end{gathered}`

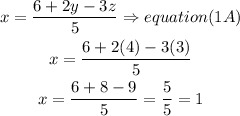
so

X=1

therefore, the answer is

X=1

Y=4

Z=3

I hope this helps you