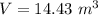Question

what is the value of right triangle pyramid whose is base is 5 meters on each side and whose altitude 4 meters round to the nearest hundredth

Answer 1

The volume of the right triangle pyramid is;

`V=14.43\text{ }m^3`

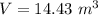
Step-by-step explanation:

Given the right triangle pyramid whose base is 5 meters on each side and whose altitude 4 meters.

`\begin{gathered} H=4 \\ a=b=c=5 \end{gathered}`

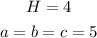
Recall that the area of a pyramid can be calculated using the formula;

`V=(1)/(3)AH`

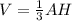
where;

A is the area of the base of the pyramid and H the altitute of the pyramid.

The area of the triangular base is;

`A=(1)/(2)bh`

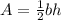
the height of the base is;

`\begin{gathered} h=\sqrt[]{5^2-2.5^2} \\ h=\sqrt[]{18.75} \\ h=4.33\text{ m} \end{gathered}`

substituting to calculate the Volume of the pyramid;

`\begin{gathered} V=(1)/(3)AH \\ V=(1)/(3)((1)/(2)bh)H \\ V=(1)/(6)\text{bhH} \\ b=5\text{ m} \\ h=4.33\text{ m} \\ H=\text{ 4 m} \\ so; \\ V=(1)/(6)*5*4.33*4 \\ V=14.43\text{ }m^3 \end{gathered}`

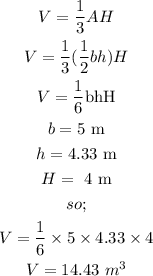
Therefore, the volume of the right triangle pyramid is;

`V=14.43\text{ }m^3`