Given: A exponential function-
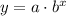
passing through the points (1,6) and (2,9)
Required: To find out the value of a and b.
Explanation: Since the given exponential function is passing through (1,6)
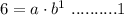
Now the function is also passing through (2,9)
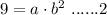
Dividing eq 2 and eq 1 we get,
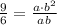
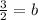
Putting this value of b in eq 1,
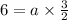
This gives,
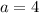
Final answer: The value of a=4 and b=1.5