Question

Determine if negative pi over 6 and 46 divided by 12 are coterminal. show or explain your work

Answer 1

Two angles are coterminal if they end up in the same ray if they are given in standard position (they both begin in the positive x-axis).

To find out if two angles are coterminal we can add or substract a whole revolution (2pi) or more revolutions to one of them and we need to get the other one.

In this case we will need that the equation:

`2\pi n-(\pi)/(6)=(46)/(12)\pi`

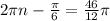
has an integer solution for n. This will mean that we can go from one angle to the other with a given number of revolutions.

Solving for n we have:

`\begin{gathered} 2\pi n-(\pi)/(6)=(46)/(12)\pi \\ 2\pi n=(46)/(12)\pi+(\pi)/(6) \\ 2\pi n=(48)/(12)\pi \\ 2\pi n=4\pi \\ n=(4\pi)/(2\pi) \\ n=2 \end{gathered}`

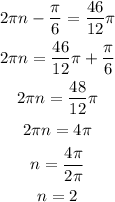
This means that if we begin in the angle -pi/6 and give two whole revolutions we end up in the angle 46/12pi.

Therefore, the angles are coterminal.