Question

Use U-Substitution to solve the following polynomial. 4x^4 + 2x^2 - 12 = 0

Answer 1

`x=\sqrt[]{(3)/(2)},x=-\sqrt[]{(3)/(2)},x=\sqrt[]{2}i,x=-\sqrt[]{2}i`

Step-by-step explanation

We want to solve the given polynomial by U-Substitution:

`4x^4+2x^2-12=0`

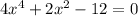
To do this, we make the following substitution:

`u=x^2`

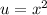
The polynomial then becomes:

`4u^2+2u-12=0`

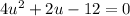
Solve the quadratic equation by factorization:

`\begin{gathered} 4u^2+8u-6u-12=0 \\ \Rightarrow4u(u+2)-6(u+2)=0 \\ \Rightarrow(4u-6)(u+2)=0 \\ \Rightarrow4u-6=0;u+2=0 \\ \Rightarrow4u=6;u=-2 \\ u=(6)/(4)=(3)/(2);u=-2 \end{gathered}`

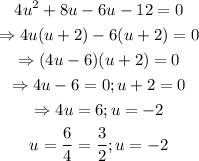
Recall that:

`\begin{gathered} u=x^2 \\ \Rightarrow x=\pm\sqrt[]{u} \end{gathered}`

Therefore, we have that:

`\begin{gathered} x=\pm\sqrt[]{(3)/(2)};x=\pm\sqrt[]{-2}=\pm\sqrt[]{2\cdot-1} \\ x=\pm\sqrt[]{(3)/(2)};x=\pm\sqrt[]{2}i \\ \Rightarrow x=\sqrt[]{(3)/(2)},x=-\sqrt[]{(3)/(2)},x=\sqrt[]{2}i,x=-\sqrt[]{2}i \end{gathered}`

Those are the solutions of the polynomial.