Question

The difference in length of a spring on a pogo stick from its non-compressed length when a teenager is jumping on it after 6 seconds can be described by the function#(6) f(theta)= 2cos(theta) + sqrt(3).Part A: Determine all values where the pogo stick's spring will be equal to its non-compressed length. (5 points)Part B: If the angle was doubled, that is theta became 2theta what are the solutions in the interval [0, 211)? How do these compare to the original function? (5 points)Part C: A toddler is jumping on another pogo stick whose length of their spring can be represented by the function g(8) = 1-

Answer 1

`\begin{gathered} A)\theta=(\pi)/(2)+2\pi n,\:θ=(3\pi)/(2)+2\pi n \\ B)\theta=(5\pi)/(12),(7\pi)/(12),(17\pi)/(12),(19\pi)/(12) \end{gathered}`

A) Let's begin by writing out the equation for the given condition:

`\begin{gathered} f(\theta)=2\cos(\theta)+√(3) \\ 2\cos(\theta)+√(3)=√(3) \\ 2\cos(\theta)=0 \\ θ=(\pi )/(2)+2\pi n,\:θ=(3\pi )/(2)+2\pi n \end{gathered}`

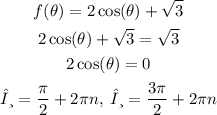
Notice that in part A, we're determining all values in which the pogo stick is equal to its non-compressed length.

B) This part consists in solving the following equation:

`\begin{gathered} 2\cos \left(2θ\right)+√(3)=0,\:0\le \:θ<2\pi \\ 2\cos \left(2θ\right)+√(3)-√(3)=0-√(3) \\ 2\cos \left(2θ\right)=-√(3) \\ (2\cos \left(2θ\right))/(2)=(-√(3))/(2) \\ \cos \left(2θ\right)=-(√(3))/(2) \\ 2θ=(5\pi )/(6)+2\pi n \\ (2θ)/(2)=((5\pi )/(6))/(2)+(2\pi n)/(2) \\ θ=(5\pi )/(12)+\pi n \\ \\ 2θ=(7\pi )/(6)+2\pi n \\ (2θ)/(2)=((7\pi )/(6))/(2)+(2\pi n)/(2) \\ θ=(7\pi )/(12)+\pi n \\ \theta=(5\pi)/(12),\:θ=(7\pi)/(12),\:θ=(17\pi)/(12),\:θ=(19\pi)/(12) \end{gathered}`

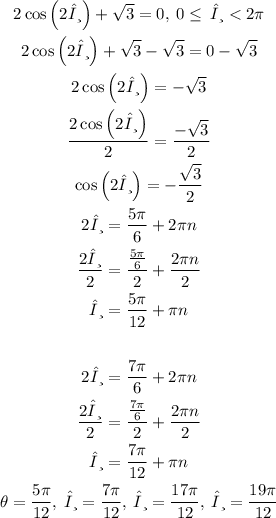
Note that since the pogo has a periodical movement and an interval was defined then the solutions above are defined for the interval.