Consider the following diagram,
Let 'y' be the side of the garden. And 'x' be the side of the square formed by the walkway.
Given that the garden is a square with perimeter 260 feet,
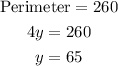
From the above diagram, it can be observed that,
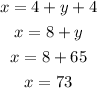
Consider that the area of a square is given by,
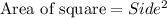
The area of the inner square i.e. garden will be,
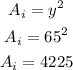
The area of the outer square will be,
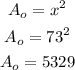
The difference between the area will give the area of the walkway (A), that can be calculated as,
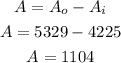
Thus, the area of the walkway is 1104 square feet.