Given in the question:
a.) Vince puts 400.00 into an account.
b.) The account earns 15% interest compounded monthly.
c.) How much will be in the account after 6 years?
For this type of interest problem, since been mentioned that this is a compounded interest, we will be using the compounded interest formula:
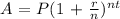
Where,
A = Amount after a certain amount of time.
P = Principal/Initial Amount = 400
r = Interest Rate (In Decimal Form) = 15%/100% = 0.15
n = Number of times interest is compounded = Monthly = 12
t = Time (In Years) = 6 years
Let's plug in the values in the formula to be able to get the value of A.
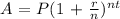
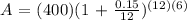
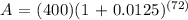
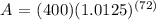
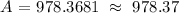
Therefore, Vince's account will be 978.37 after 6 years.