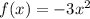Step 1. We start by looking at the graph of the function:
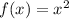
The graph is:
Step 2. The horizontal axis is the x-axis, and to reflect the original graph (the graph from step 1) over the x-axis, we add a negative sign next to the x^2:
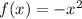
We can look at the resulting graph to confirm that the graph has now been reflected over the x-axis:
Step 3. We have reflected the graph over the x-axis but we still need to stretch it by a factor of 3.
We can stretch the graph of a quadratic function by multiplying the squared term by the factor, in this case by 3.
The resulting equation is:
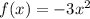
And the graph will finally look as follows:
Answer: