Question

use four rectangles to estimate the area between the graph of the function f(x) = V9x + 6 and the x-axis on the interval[0, 4] using the right endpoints of the subintervals as the sample points. Round any intermediate calculations, if needed, toless than six decimal places, and round your final answer to three decimal places.

Answer 1

20.997

1) Let's start by dividing from 0 to 4 into n equal subintervals:

`n=4,x=((4-0))/(4)=1`

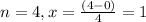
So the width of each rectangle is going to be 1

2) The next step is to calculate the area below the curve using the right endpoints using the following intervals:

`\lbrack0,1\rbrack,\lbrack1,2\rbrack,\lbrack2,3\rbrack,\lbrack3,4\rbrack`

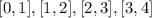
And plug each endpoint into that we have:

`\begin{gathered} R_4=f(x_1)\cdot x+f(x_2)x+f(x_3)x+f(x_4)x \\ R_4=f(1)\cdot1+f(2)\cdot1+f(3)\cdot1+f(4)\cdot1 \\ R_4=(\sqrt[]{9(1)+6})\cdot1+(\sqrt[]{9(2)+6})\cdot1+(\sqrt[]{9(3)+6})\cdot1+(\sqrt[]{9(4)+6})\cdot1 \\ R_4=\sqrt[]{15}+2\sqrt[]{6}+\sqrt[]{33}+\sqrt[]{42}\approx20.997 \end{gathered}`

Note that since each rectangle has a width of 1 unit, we could plug it into that.

3) Hence, the answer is approximately 20.997