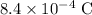Question

5. A particle of unknown charge obtains 0.042 J of kinetic energy as it moves from point A to point B. Point Ahas an electric potential of 700.0 V; and point B has an electric potential of 200.0 V. Determine the magnitudeand sign of the charge.

Answer 1

Given:

The kinetic energy of the charged particle is,

`\Delta U=0.042\text{ J}`

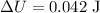
Point A has electric potential,

`V_A=700.0\text{ V}`

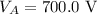
The potential at point B is,

`V_B=200.0\text{ V}`

To find:

The magnitude and the sign of the charge

Step-by-step explanation:

The energy of the charged particle is,

`q\Delta V`

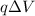
which is equal to,

`\Delta U`

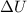
As the charged particle is moving from higher to lower potential region, the charge is positive. So, we can write,

`\begin{gathered} q(V_A-V_B)=0.042 \\ q(700.0-200.0)=0.042 \\ q=(0.042)/(700.0-200.0) \\ q=8.4*10^(-4)\text{ C} \end{gathered}`

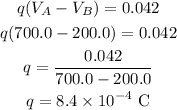
Hence, the charge is positive and the magnitude is,

`8.4*10^(-4)\text{ C}`