The given function is f(x) and g(x).
The rate of change of f(x) in the interval -2 to 2 can be determied as,
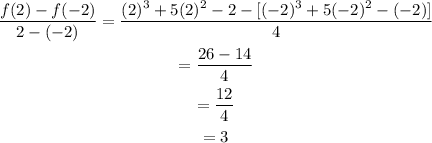
The rate of change of f(x) is positive hence its value will increase in the interval -2 to 2.
The rate of change of g(x) in the interval -2 to 2 can be determined as,
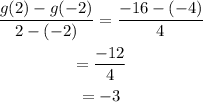
The rate of change of g(x) is negative hence its value will decrease in the interval -2 to 2.
The rate of change of f(x) and g(x) are numerically the same.
Thus, the rate of change of f(x) and g(x) are the same but f(x) increases and g(x) decreases in the interval -2 to 2.
Thus, Option (B) is the correct solution.