Question

Kelly buys 3 video games that cost $18.96 each. She also buys 2 pairs of earbuds that cost $11.50 each. She has a coupon for $2 off the price of each video game. Kelly us a calculator, as shown, to find that the total cost of the items is $77.85. The cashier tells her that the total cost is $73.85. Who is correct? Justify your argument.

Answer 1

The cashier is correct.

Kelly is wrong because he calculated the coupon as 1 and deducted only $2 from the total price of goods instead of calculating the total amount of coupon and deducting from the total price of goods.

Note that the coupon is $2 off the price of each video game

Step-by-step explanation:

Let run through the sum of the goods Kelly bought;

3 video games that cost $18.95 each;

`3*$18.95$=\text{ \$56.85}`

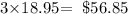
2 pairs of earbuds that cost $11.50 each;

`2*11.50=\text{ \$23}`

Total is;

`\text{ \$56.85}+\text{ \$23}=\text{ \$79.85}`

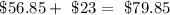
Given that She has a coupon for $2 off the price of each video game.

For the 3 video games, the coupon is;

`3*\text{ \$2}=\text{ \$6}`

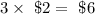
The total cost will then be the total price of goods minus the coupon;

`\begin{gathered} C=\text{ \$79.85}-\text{ \$6} \\ C=\text{ \$73.85} \end{gathered}`

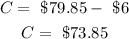
Therefore, the cashier is correct.

Kelly is wrong because he calculated the coupon as 1 and deducted only $2 from the total price of goods instead of calculating the total amount of coupon and deducting from the total price of goods.

Note that the coupon is $2 off the price of each video game