Statement 1:
Let the smaller number be x
Let the larger number be y
The difference between two whole numbers is 2 can be written as
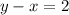
Statement 2:
Two times the square of the smaller number is:
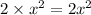
Three times the square of the larger number is:
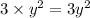
Thus,
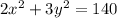
Therefore we would solve the system of equations to find the two numbers
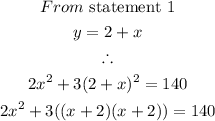
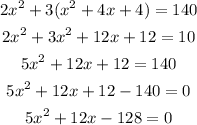
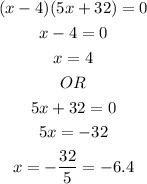
To find y, we would use x =4, because the statement said the numbers are whole numbers
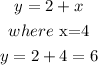
Hence, the numbers are 4 and 6