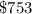Question

Suppose you invest $500 at an annual interest rate of 4.1% compounded continuously. How much will you have in the account after 10 years?Substitute the values into the continuously compounded interest formula, A = Pert.How much will you have in the account after 10 years? Round the solution to the nearest dollar.

Answer 1

We will investigate the continuous compounding evaluation of an initial investment.

The formulation used for continuous compounding to express the future value ( A ) is represented by:

`A\text{ = P}\cdot e^(r\cdot t)`

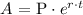
Where,

`\begin{gathered} P\colon\text{ Present Value} \\ r\colon\text{ Rate ( Annual )} \\ t\colon time\text{ in years} \end{gathered}`

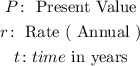
The following investment ( P ) was made at an anual interest ( r ). We are to determine the amount in the bank account after ( t ) years from now:

`P\text{ = \$500 , r = 4.1\% , t = 10 years }`

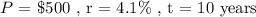
The amount accumulated in the bank account can be determined from the given formulation as follows:

`\begin{gathered} A\text{ = 500}\cdot e^{(4.1)/(100)\cdot10} \\ A\text{ = 500}\cdot e^(0.41) \\ A\text{ = }753.40889 \end{gathered}`

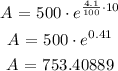
The solution rounded to the nearest dollar is:

`\text{\$}753`