To answer this question, we know that the percentage can be expressed as follows:
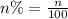
Now, if we know that the n percent of 221 is 79.4, we can write the following equation:
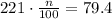
To solve this, we can multiply both sides by (100/221). Then we have:
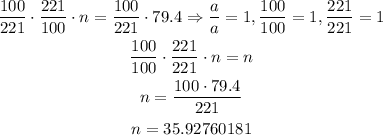
Now, we can see that 79.4 is 35.92..percent of 221.
If we round the percentage to the tenth place, we have 35.9.
In summary, we can say that 79.4 is 35.9% of 221.