The two triangles, ABC and FGH are congruent.
The length of two corresponding sides are given,
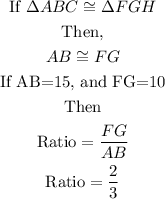
If the ratio of the sides is determined as 2/3, then the perimeter which is an addition of all three sides shall be;

To determine the area, we shall apply the ratio raied to the power of 2 (becaue the area i in units squared).
Therefore, we would have;
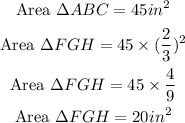
Therefore, the perimeter of triangle FGH is 24 inches
The area of triangle FGH is 20 inches squared