Question

Is M the midpoint of AB? (A is at (-4,5), M is at (4,9) and B is at (12,13)).

Answer 1

Yes, M is the midpoint of AB

Step-by-step explanation

To know if M is the midpoint of AB, we have to see if the distance from A to M is the same distance from M to B.

The distance between two points (x1, y1) and (x2, y2) is:

`d=\sqrt[]{(x_1-x_2)^2+(y_1-y_2)^2}`

The distance AM is:

`\begin{gathered} d_(AM)=\sqrt[]{(-4-4)^2+(5-9)^2} \\ d_(AM)=\sqrt[]{8^2+4^2} \\ d_(AM)=\sqrt[]{64+16} \\ d_(AM)=\sqrt[]{80} \\ d_(AM)=4\sqrt[]{5} \end{gathered}`

The distance MB is:

`\begin{gathered} d_(MB)=\sqrt[]{(4-12)^2+(9-13)^2} \\ d_(MB)=\sqrt[]{8^2+4^2} \\ d_(MB)=\sqrt[]{64+16} \\ d_(MB)=\sqrt[]{80} \\ d_(MB)=4\sqrt[]{5} \end{gathered}`

Then

`d_(AM)=d_(MB)`

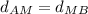
Therefore M is the midpoint of AB