Question

Can you help answer this problem with the steps you took to solve?

Answer 1

a.

To determine the degree of the polynomial we just need to add the powers of x, then we have:

`3+2+1+1=7`

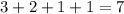
Therefore, the degree of the polynomial is 7

b.

We know that any polynomial function can be writen as:

`f(x)=(x-a_1)(x-a_2)(x-a_3)\cdots(x-a_(n-1))(x-a_n)`

where ai are the zeros of the polynomial. The function given is already given in this form, then we have that the zeros of the function are:

`\begin{gathered} x=-8165 \\ x=762 \\ x=574398 \\ x=-351 \end{gathered}`

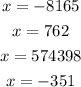
To determine the end behaviour of the function (when x is extremely large or extremely small) we just need to look at two things:

• If the larger power of x is even then the end behaviour will have the same sign of the leading coefficient; on the other hand, if the larger powers is odd then the end behaviour will have opposite sign to the leading coefficient.

,

• The sign of the leading coefficient.

In this case the larger power of x is seven and the leading coefficient is negative. With this in mind we can answer the last two parts.

c.

In this case as x approaches minus infinity then the function will approach positive infinity.

d.

For this function, as x approaches infinity, then the function will approach minus infinity.