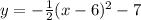given data:
vertex at V(6, −7)
passes through point P(4, −9).
In general a parabola in vertex(h,k) form can be written as:
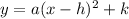
Thus,
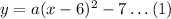
Since, the point P(4, −9) passes through the parabola,
we can write as follows and solve the equation to find the value of a,

Thus, subsitute in the equation (1) to get the quadratic equation,