Question

(a) Use the empirical rule to estimate the number of farms whose land and building values per acre are between $1500 and $1700. round to nearest whole number if needed (B) If additional farms were sampled, about how many of these additional farms would you expect to have land and building values between $1500 per acre and $1700 per acre? round to nearest whole number if needed

Answer 1

GIVEN:

We are given the mean and standard deviation for a sample size of 77 land and buildings per acre as follows;

`\begin{gathered} Mean=1600 \\ \\ Standard\text{ }deviation=100 \\ \\ n=77 \end{gathered}`

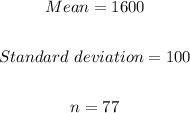
Required;

(a) To estimate the number of farms whose land and building values per acre are between ​$1500 and ​$1700.

(b) If 21 additional farms were​ sampled, about how many of these additional farms would you expect to have land and building values between ​$1500 per acre and ​$1700 per​ acre?

Step-by-step solution;

The empirical rule states that for a bell shaped distribution, the deviation from the mean follows the pattern below;

`\begin{gathered} 1\text{ }standard\text{ }deviation\text{ }from\text{ }the\text{ }mean=68\% \\ \\ 2\text{ }standard\text{ }deviations\text{ }from\text{ }the\text{ }mean=95\% \\ \\ 3\text{ }standard\text{ }deviations\text{ }from\text{ }the\text{ }mean=99.7\% \end{gathered}`

Looking at the range given, we can determine the following;

`\begin{gathered} 1500=1600-1(100) \\ \\ 1500=mean-1(standard\text{ }deviation) \end{gathered}`
`\begin{gathered} 1700=1600+1(100) \\ \\ 1700=mean+1(standard\text{ }deviation) \end{gathered}`

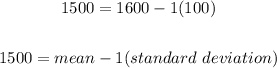
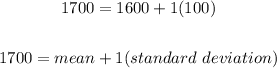
We can now see that the data is 1 standard deviation from the mean (both at the upper limit and the lower limit).

Using the empirical rule as summarized above, we can safely say 68% of the sample size will lie between $1500 and $1700.

Therefore, we can calculate as follows;

`\begin{gathered} n=77 \\ \\ Number\text{ }of\text{ }farms=77*68\% \\ \\ Number\text{ }of\text{ }farms=77*0.68 \\ \\ Number\text{ }of\text{ }farms=52.36 \\ \\ Number\text{ }of\text{ }farms\approx52\text{ }(rounded\text{ }to\text{ }the\text{ }nearest\text{ }whole\text{ }number) \end{gathered}`

This means,

(A) Approximately 52 farms will have their values between $1500 and $1700 per acre.

If the sample size were increased by 21 additional farms, that is;

`\begin{gathered} Sample\text{ }size=77+21 \\ \\ n=98 \end{gathered}`
`\begin{gathered} Number\text{ }of\text{ }farms=98*68\% \\ \\ Number\text{ }of\text{ }farms=98*0.68 \\ \\ Number\text{ }of\text{ }farms=66.64 \\ \\ Number\text{ }of\text{ }farms\approx67 \end{gathered}`

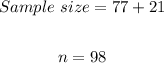
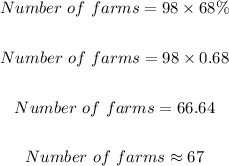
Since we are concerned about the "additional 21,"

`\begin{gathered} Farms\text{ }between\text{ }1500\text{ }and\text{ }1700=98-67 \\ \\ Farms\text{ }between\text{ }1500\text{ }and\text{ }1700=31 \end{gathered}`

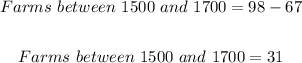
Therefore,

ANSWER:

(A) The number of farms whose land and building values per acre are between ​$1500 and ​$1700 is 52 (rounded to the nearest whole number)

(B) Additional farms you would expect to have land and building values between ​$1500 per acre and ​$1700 per​ acre is 31.