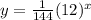Solution:
Given the general exponential function expressed as
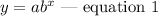
If the function passes through the points (x₁, y₁) and (x₂, y₂), we can defined the exponential function by solving for a and b.
This is done by substituting the values of x and y into the general exponential function as shown below:

Given that the graph of the exponential function passes through (2,1) and (3,12), this implies that
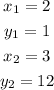
Thus, substituting the x and y values into equation 1 , as done in equation 2 and 3, we have
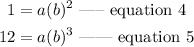
Divide equation 5 by equation 4,
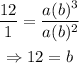
Substitute the obtained value of b into either equation 4 or 5.
Substituting into equation 4, we have
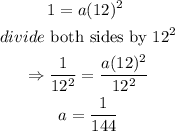
Substitute the obtained values of a and b into equation 1.
From equation 1,
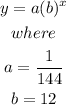
Thus, the exponential function is expressed as