Question

The difference of the square of a number and 10 is equal to 3 times that number. Findthe negative solution.

Answer 1

Let the number be x.

The first part of the question can be written as

`x^2-10`

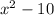
Adding the other part of the question, we have

`x^2-10=3x`

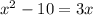
Rewriting the equation, we have

`x^2-3x-10=0`

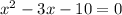
Next, we solve the quadratic equation.

By factorization, we replace -3x with -5x and 2x. Hence

`\begin{gathered} x^2-5x+2x-10=0 \\ x(x-5)+2(x-5)=0 \\ (x-5)(x+2)=0 \\ \therefore \\ x=5\text{ or -2} \end{gathered}`

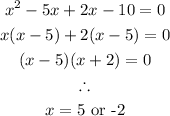
Therefore, the negative solution is -2.