Question

For the function #1, (a) find a simplified form of the difference quotient and (b) complete the following table.

Answer 1

`\frac{f(x+h)-f(x)_{}}{h}`

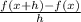
To determine the difference quotient, here are the steps.

1. To get f(x + h), replace the "x" with "x + h" in the function.

`\begin{gathered} f(x+h)=7(x+h)^2_{} \\ f(x+h)=7(x^2+2xh+h^2)_{} \\ f(x+h)=7x^2+14xh+7h^2_{} \end{gathered}`

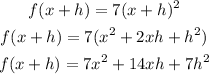
2. Now that we have the value of f(x + h), together with the value of f(x), let's plug them in the difference quotient above.

`\begin{gathered} \frac{f(x+h)-f(x)_{}}{h}_{} \\ ((7x^2+14xh+7h^2)-(7x^2))/(h) \end{gathered}`

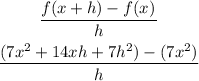
3. Simplify the equation.

`\begin{gathered} =(7x^2+14xh+7h^2-7x^2)/(h) \\ =(14xh+7h^2)/(h) \\ \text{Factor out }h\text{ in the numerator.} \\ =\frac{h(14x+7h)_{}}{h} \\ \text{Cancel h.} \\ =14x+7h \end{gathered}`

Therefore, the simplified form of the difference quotient for item 1 is 14x + 7h.

To complete the table, let's plug in the given values of x and h to the simplified form of the difference quotient.

At x = 4 and h = 2.

`\begin{gathered} =14x+7h \\ =14(4)+7(2) \\ =56+14 \\ =70 \end{gathered}`

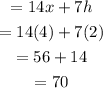
At x = 4 and h = 1.

`\begin{gathered} =14x+7h \\ =14(4)+7(1) \\ =56+7 \\ =63 \end{gathered}`

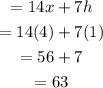
At x = 4 and h = 0.1

`\begin{gathered} =14x+7h \\ =14(4)+7(0.1) \\ =56+0.7 \\ =56.7 \end{gathered}`

At x = 4 and h = 0.01

`\begin{gathered} =14x+7h \\ =14(4)+7(0.01) \\ =56+0.07 \\ =56.07 \end{gathered}`

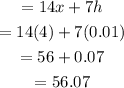
Completing the table, we have: