Question

8. Values of a Function The graph of a function g is given.(a) Find g(-4),g(-2),g(0),g(2), and g(4) (b) Find the domain and range of g.(c) Find the values of x for which g(x) = 3 .(d) Estimate the values of x for which g(x) <= 0 .(e) Find the net change in g between x = - 1 and x = 2 .V

Answer 1

#8

(a)

We have to find several functional values for each value of x given.

For that, we go to that x-value in the axis, then see what is the corresponding y-value in the function. That is out answer.

From the graph,

`\begin{gathered} g(-4)=3 \\ g(-2)=2 \\ g(0)=-2 \\ g(2)=1 \\ g(4)=0 \end{gathered}`

(b)

The domain is the set of x-values for which a function is defined.

The range is the set of y-values for which a function is defined.

Looking at the graph, we see that the function g is defined from x = - 4 to x = 4.

Also, looking at the graph, we see that the function g is defined from y = - 2 to y = 3

Now, we can write the domain and range as:

`\begin{gathered} D=-4\leq x\leq4 \\ R=-2\leq y\leq3 \end{gathered}`

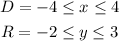
(c)

We can draw a line y = 3 and see where it cuts the graph of the function g. At those specific points (x) are our answers to this part.

Let's see the graph:

So, for x = -4, the function has a value of 3.

`\begin{gathered} g(x)=3 \\ \text{For} \\ x=-4 \end{gathered}`

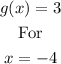
(d)

We need to find the values of x for which g(x) is less than or equal to 0.

We will draw a line y = 0 (x-axis) and see where (from which x to which x) the function is beneath the line.

The graph:

From the graph, we can see that from x = -1 to x ≈ 1.8 (approximate) , the function is less than or equal to 0.

`\begin{gathered} \text{For} \\ -1\leq x\leq1.8 \\ g(x)\leq0 \end{gathered}`

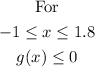
(e)

We will find the functional values at x = - 1 and x = 2 and then find the difference. That is the net change.

From the graph, we see that:

When x = -1, the functional value is "0".

When x = 2, the functional value is "1".

The net change is 1 - 0 = 1.