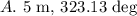Question

7. Given the vectors A = 4 m east and B = 3 m south, using graphical addition determine which of the following most likely represent the magnitude and direction of the sum vector (A + B) respectively. (You should be able to answer it with sketches not drawn to scale.) (1 point)A. 5 m, 323.13 degB. 7 m, 323.13 degC. 5 m, 216.87 degD. 5 m, 36.87 degE. 7 m, 216.87 deg

Answer 1

`A.\text{ }5\text{ m, }323.13\text{ deg}`

Step-by-step explanation

First, let us make a sketch of the vectors:

The thick black line represents the vector sum of the two vectors A and B.

We see that the coordinates of the vector (A + B) are:

`(A+B)=(4,-3)`

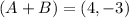
We can write it in component form as:

`A+B=4i-3j`

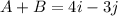
To find the magnitude of (A + B), we have to find the length of the line using the formula:

`L=|A+B|=√(x^2+y^2)`

where (x, y) are the coordinates of the vector.

Hence, the magnitude of the vector is:

`\begin{gathered} |A+B|=√((4)^2+(-3)^2)=√(16+9) \\ \\ |A+B|=√(25) \\ \\ |A+B|=5\text{ m} \end{gathered}`

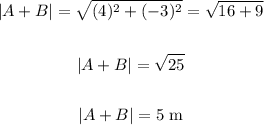
To find the direction of the vector (A + B), we have to apply the formula:

`\theta=\tan^(-1)((y)/(x))`

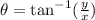
Therefore, the direction of the vector is:

`\begin{gathered} \theta=\tan^(-1)(-(3)/(4)) \\ \\ \theta=143.13\text{ deg or }323.13\text{ deg} \end{gathered}`

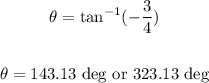
Since the vector is in the fourth quadrant, then, the direction is:

`\theta=323.13\text{ deg}`

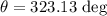
Therefore, the magnitude and direction of the sum vector (A + B) are:

`A.\text{ }5\text{ m, }323.13\text{ deg}`