Question

A scientist has two solution , which she has labeled solution A and solution B. Each contains salt. she knows that solution A is 65% salt and solution B is 90% salt she want to obtain 180 ounces of a mixture that is 70% salt. how many ounces of each solution should she use

Answer 1

he will need 171 ounces of solution A

he will need 9 ounces of solution B

Step-by-step explanation

Step 1

Let

x represents the number of ounces of solution A in the mixture

y represents the number of ounces of solution B in the mixture

then

`x+y=180\text{ Equation(1)}`

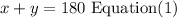
Also

`\begin{gathered} \text{salt in the mixture from solution A= x}\cdot0.65 \\ \text{salt in the mixture from solution B=y}\cdot0.9 \\ so \\ \text{salt in the mixture from solution A+salt in the mixture from solution B=180}\cdot0.7 \\ \text{replacing} \\ 0.65x+0.9y=180\cdot0.7 \\ 0.65x+0.9y=126\text{ Equation (2)} \end{gathered}`

Step 2

find x and y using equation (1) and equation(2)

i)isolate x in equation (1)

`\begin{gathered} x+y=180\text{ Equation(1)} \\ x+y=180 \\ \text{subtract y in both sides} \\ x+y-y=180-y \\ x=180-y\text{ Equation(3)} \end{gathered}`

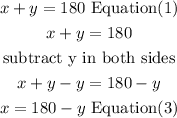
ii)replace equation (3) into equation (2)

`\begin{gathered} 0.65x+0.9y=126\text{ Equation (2)} \\ 0.65x+0.9y=126\text{ } \\ 0.65(180-y)+0.9y=126 \\ 117-0.65y+0.9y=126 \\ 0.25y+117=126 \\ \text{subtract 117 in both sides} \\ 0.25y+117-117=126-117 \\ 0.25y=9 \\ y=(9)/(0.25) \\ y=9 \end{gathered}`

so, he will need 9 ounces of solution B

Step 3

finally, replace the value of y =9 in equation (1) to find x

`\begin{gathered} x+y=180 \\ x+9=180 \\ x=180-9 \\ x=171 \end{gathered}`

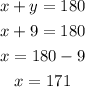
he will need 171 ounces of solution A