Question

A ball starts rolling to the right with a velocity +5.00 m/s. Because it is rolling up a hill, the velocity will decrease until the ball eventually stops and then rolls back down the ramp, past the point where it started, and on down to the left. The acceleration of the ball is -1.81 m/s2. How much time will pass before the ball has reached the point that is Δ=−2.00 m from where it started?

Answer 1

We know that the acceleration of the ball is constant, this means that the motion is an uniformly accelerated motion and hence we can use one of the following equations:

`\begin{gathered} a=(v_f-v_0)/(t) \\ \Delta x=v_0t+(1)/(2)at^2 \\ v_f^2-v_0^2=2a\Delta x \end{gathered}`

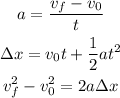
Now, in this case we know we want to know the time and we know:

• The initial velocity 5 m/s

,

• The acceleration -1.81 m/s²

,

• The change in position of the object -2 m

Comparing what we want and what we know we notice that we can use the second equation, plugging the values and solving for t we have:

`\begin{gathered} -2=5t+(1)/(2)(-1.81)t^2 \\ -2=5t-0.905t^2 \\ 0.905t^2-5t-2=0 \\ \text{ Using the quadratic formula we have:} \\ t=(-(-5)\pm√((-5)^2-4(0.905)(-2)))/(2(0.905)) \\ t=(5\pm√(32.24))/(1.81) \\ \text{ Then:} \\ t=(5+√(32.24))/(1.81)=5.90 \\ \text{ or} \\ t=(5-√(32.24))/(1.81)=-0.37 \end{gathered}`

Choosing the positive solution (since the time is always positive) we conclude that it takes 5.90 s for the ball to be two meters to the left from where it started.