Ksp is a constant that gives the following:
For the solution of AgBr:
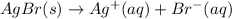
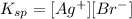
So, given an initial pure water, let s be the solubility of AgBr. If we add s of AgBr, it will dossiciate into s Ag⁺ and s Br⁻, so, for a saturated solution of AgBr, we have:
![\begin{gathered} \lbrack Ag^+\rbrack=s \\ \lbrack Br^-\rbrack=s \\ K_(sp)=s\cdot s \\ K_(sp)=s^2 \\ s=\sqrt[]{K_(sp)}=\sqrt[]{5.0*10^(-13)}M=\sqrt[]{0.50*10^(-12)}M=\sqrt[]{0.50}*10^(-6)M=0.70710\ldots*10^(-6)M\approx7.1*10^(-7)M \end{gathered}]()
So, the solubility of AgBr is approximately 7.1 x 10⁻⁷ M.