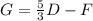Solve for G.D=3/5(F+G)

Question

asked Dec 16, 2023 86.5k views

1 Answer

Monkey · Answer 1 · 2023-12-22T11:24:21+0000

The equation given is

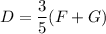
$\begin{gathered} D=(3)/(5)(F+G) \\ \end{gathered}$

We multiply the "3/5" with both F and G following the distributive property,

Now we take the term with "G" to one side and solve with the rules of algebra. We isolate G:

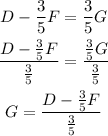
$\begin{gathered} D-(3)/(5)F=(3)/(5)G \\ (D-(3)/(5)F)/((3)/(5))=((3)/(5)G)/((3)/(5)) \\ G=(D-(3)/(5)F)/((3)/(5)) \end{gathered}$

We dividing by a fraction, we can multiply by its reciprocal. It doesn't change anything.

So, further simplifying, we have:

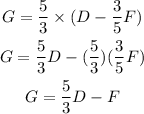
$\begin{gathered} G=(5)/(3)*(D-(3)/(5)F) \\ G=(5)/(3)D-((5)/(3))((3)/(5)F) \\ G=(5)/(3)D-F \end{gathered}$ Final Answer