Question

While on a walk in the country you pass a field full of horses and geese after a quick count you determine there are 30 heads and 82 feet in the field how many of each animal are there?

Answer 1

19 geese and 11 horses

1) Note that geese and horses have each one, one head. So we can solve this problem by setting a system of Linear equations:

1 horse: 4 feet

1 goose: 2 feet

`\begin{gathered} g+h=30 \\ 2g+4h=82 \end{gathered}`

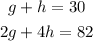
Notice the second equation relates to the number of feet each animal has.

2) We can solve this by using the Elimination Method, multiplying the first equation by -2

`\begin{gathered} g+h=30 \\ 2g+4h=82 \\ --------- \\ -2g-2h=-60 \\ 2g+4h=82 \\ ------------- \\ 2h=22 \\ h=11 \end{gathered}`

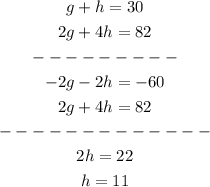
Now, we can plug into the 1st equation h=11

`\begin{gathered} g+h=30 \\ g+11=30 \\ g+11-11=30-11 \\ g=19 \end{gathered}`

So, there are 19 geese and 11 horses.