Question

Factor f(x) into linear factors given that k is a zero of f(x).Factor f(x) = 2x^3 - 3x^2 - 5x+6; k=1

Answer 1

The given function is

`f(x)=2x^3-3x^2-5x+6`

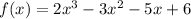
Since k = 1 is a zero of f(x), that means

That means f(x) = 0 at x = 1

Let us find the factor from x = 1

`\begin{gathered} x=1 \\ x-1=1-1 \\ x-1=0 \end{gathered}`

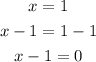
The factor is (x - 1)

We will divide f(x) by (x - 1) to find the other factors

`\begin{gathered} (2x^3-3x^2-5x+6)/(x-1)= \\ (2x^3)/(x)=2x^2 \end{gathered}`

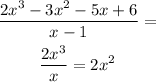
Multiply 2x^2 by (x -1 ) then subtract the answer from f(x)

`\begin{gathered} 2x^2(x-1)=2x^3-2x^2 \\ 2x^3-3x^2-5x+6-(2x^3-2x^2)=-x^2-5x-6 \end{gathered}`

Divide -x^2 by x, then multiply the answer by (x - 1), then subtract the result from the answer above

`\begin{gathered} -(x^2)/(x)=-x \\ -x(x-1)=-x^2+x \\ -x^2-5x+6-(-x^2+x)=-6x+6 \end{gathered}`

Divide -6x by x, then multiply the result by (x - 1), then subtract the answer from the last answer above

`\begin{gathered} (-6x)/(x)=-6 \\ -6(x-1)=-6x+6 \\ -6x+6-(-6x+6)=0 \end{gathered}`

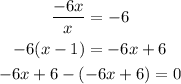
Then

`(2x^3-3x^2-5x+6)/(x-1)=2x^2-x-6`

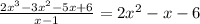
Now we will factorize it into two factors

`\begin{gathered} 2x^2=(2x)(x) \\ -6=(-2)(3) \\ (-2)(2x)+(3)(x)=-4x+3x=-x \end{gathered}`

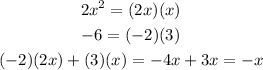
Then the 2 factors are (2x + 3) and (x - 2)

The factors of f(x) are

(x - 1) (x - 2) (2x + 3)