Question

Ammonium sulfate (NH4)2SO4 is a common substance used to treat highly alkaline soils. If a particular piece of land requires you to apply 17.2 g of ammonium sulfate how many mL of a 6.50 M ammonium sulfate solution do you need to apply to that area of land?

Answer 1

0.02 L (20 mL) of ammonium sulfate solution.

Step-by-step explanation:

Solutions => Molarity.

You can note that we have a given mass of ammonium sulfate ((NH4)2SO4) and its concentration (molar), so to solve this problem we have to understand first what is the molarity: the molarity (M) of a solution is the number of moles of solute dissolved in one liter of solution. The formula of molarity is the following:

`Molarity(M)=\frac{mole\text{s of solute}}{liter\text{s of solution}}=(mol)/(L).`

We can solve for 'liters of solution' but we don't know what is the value of moles of solute because we have the amount of solute in grams (mass).

We can find the number of moles of ammonium sulfate by using its molar mass, which is 132 g/mol. Remember that you can calculate the molar mass of a compound using the periodic table. The conversion from grams to moles will look like this:

`17.2\text{ g \lparen NH}_4)_2SO_4\cdot\frac{1\text{ mol \lparen NH}_4)_2SO_4}{132\text{ g \lparen NH}_4)_2SO_4}=0.130\text{ moles \lparen NH}_4)_2SO_4.`

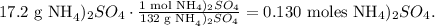
We have 0.130 moles of ammonium sulfate in 17.2 g of ammonium sulfate, so now we can replace the data that we have if we solve for 'liters of solution', like this:

`\begin{gathered} liter\text{s of solution=}\frac{moles\text{ of solute}}{molarity}\text{,} \\ \\ liter\text{s of solution=}\frac{0.130\text{ moles}}{6.50\text{ M}}\text{,} \\ \\ liters\text{ of solution=0.02 L.} \end{gathered}`

Remember that 1 L equals 1000 mL, so the conversion from 0.02 L to mL is:

`0.02\text{ L}\cdot\frac{1000\text{ mL}}{1\text{ L}}=20\text{ mL.}`

The answer would be that we need 0.02 L (20 mL) of ammonium sulfate solution to apply to the piece of land.