Question

What is the equivalent degree measure of - 11 π /12 radians written in simplest terms?165°- 165°-11 π^2/2160-1980°/12

Answer 1

To answer this question, we need to remember the conversion formula from radians to degrees. This formula is as follows:

`(180)/(\pi)(\text{rad)}=\text{degrees}`

We have, in this case, the following measure in radians:

`-(11\pi)/(12)`

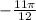
We can see that the measure is negative (the measure is in a clockwise direction), and we will have the angle in degrees, also, in a clockwise direction (negative). Then we have:

`\begin{gathered} (180)/(\pi)(-(11)/(12)\pi)=-((180)/(12))(11)((\pi)/(\pi))=-(15)(11)(1)=-165 \\ \end{gathered}`

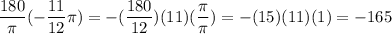
Therefore, in summary, the degree measure of - 11 π /12 is equivalent to - 165° (second option).