Given:
Maximum value = 96
Minimum value = 59.5
Median value = 59.5
Let's use the range rule of thumb to estimate the standard deviation.
The range rule of thumb states that the range is four times the standard deviation.
Thus, we have the formula:
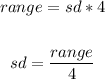
Where:
Range = Maximum value - Minimum value
To estimate the standard deviation using the range rule of thumb, we have:
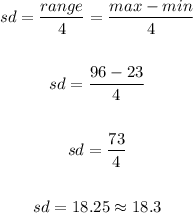
Therefore, the standard deviation is approximately 18.3
ANSWER:
18.3