Question

Carlos has been in the habit of buying a 20 ounce bottle of water at a convenience store on his way home from school every day. Each bottle costs $1.29. One of his friends tells him that at the sporting goods store in the mall there is a sale on reusable stainless steel bottles. The regular price is $29.95 but he can get one for $19.95. He can fill the reusable bottle every day with tap water, which tastes just as good as bottled water, carry it in his backpack and enjoy a cool drink at the end of the school day. Carlos doesn't mind the extra weight of carrying a full bottle with him and he believes he can save some serious money so he goes ahead and buys the reusable bottle. He wonders how much he will actually save.a. Let d represent the number of school days after buying the reusable bottle and s represent the amount of money saved. Write an equation for s as a function of d.b. In your equation, what is the slope? What does it represent in the context of the problem?c. In your equation, what is the s-intercept? What does it represent in the context of the problem?d. How much will Carlos save at the end of six weeks?e. On what day will Carlos break even?

Answer 1

a. s = -19.95 + 1.29d

b. slope = 1.29. It represents the cost of 1 non-reusable bottle of water

c. s-intercept = -19.95. It represents the cost of a reusable bottle of water

d. At the end of six weeks, he will save $18.75

e. He will break even after 16 days of school

Explanation

a.

Variables

• d: number of school days after buying the reusable bottle

,

• s: the amount of money saved

Carlos buys 1 bottle per day. Each bottle costs $1.29. Then, after d days would spend 1.29d dollars.

On the other hand, the cost of a reusable stainless steel bottle is $19.95.

If he buys the reusable bottle and avoids the cost of each non-reusable bottle of water, his savings will be:

`\begin{gathered} \text{ savings }=\text{ - reusable bottle cost + cost avoided } \\ s=-19.95+1.29d \end{gathered}`

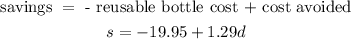
b. The slope of the line is the coefficient of the d-term, that is,

`slope=1.29`

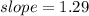
It represents the cost of 1 non-reusable bottle of water

c. The s-intercept is the constant term in the equation, that is,

`\text{ s-intercept =}-19.95`

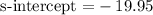
It represents the cost of a reusable bottle of water

d. Assuming that Carlos doesn't go to school at the weekends, then there are 6x5 = 30 days after 6 weeks. Substituting d = 30 into the equation:

`\begin{gathered} s=-19.95+1.29\cdot30 \\ s=-19.95+38.7 \\ s=18.75\text{ \$} \end{gathered}`

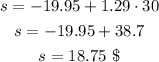
At the end of six weeks, he will save $18.75

e. If Carlos break even, his savings will be zero. Substituting s = 0 into the equation and solving for d:

`\begin{gathered} 0=-19.95+1.29d \\ 0+19.95=-19.95+1.29d+19.95 \\ 19.95=1.29d \\ (19.95)/(1.29)=(1.29d)/(1.29) \\ 16\approx d\text{ \lparen we need to round up because there are no decimal number of days\rparen} \end{gathered}`

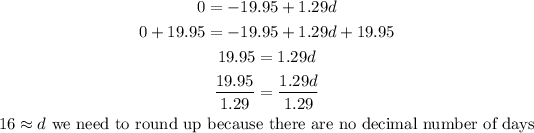
He will break even after 16 days of school