Given: The cost in dollars of making x items is given by the function C(x)=10x+700
Find: (a) The fixed cost is determined when zero items are produced.
(b) the cost of making 25 items.
(c) when maximus cost allowed $1700. the domain and range of the cost function, C(x) ?
Step-by-step explanation: (a) when zero items are produced
C(x)=10x+700
put x=0
C(x)=700
(b) the cost of making 25 items are
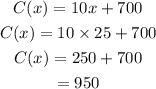
(c) maximum cost allowed is $ 1700,
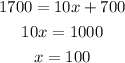
so the domain is [0,100] and range is [700,1700].