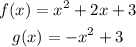Question

Which set of systems of equations represents the solution to the graph?upward opening parabola passing through negative 2 comma 3 to a minimum at negative 1 comma 2 and then increasing to 0 comma 3 and a downward opening parabola passing through negative 2 comma negative 1 to a maximum at 0 comma 3 and then decreasing through the point 2 comma negative 1 f(x) = –x2 + 2x + 3g(x) = x2 + 3 f(x) = x2 + 2x – 3g(x) = –x2 – 3 f(x) = x2 + 2x + 3g(x) = –x2 + 3 f(x) = –x2 + 2x + 3g(x) = x2 – 3

Answer 1

Use the vertex form to write the equation of each parabola:

`\begin{gathered} y=a(x-h)^2+k \\ \\ Vertex:(h,k) \end{gathered}`

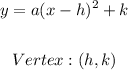
Blue parabola:

Vertex: (-1,2)

`\begin{gathered} y=a(x-(-1))^2+2 \\ y=a(x+1)^2+2 \end{gathered}`

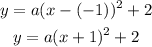
Use a point in the parabola to find the value of a:

`\begin{gathered} (0,3) \\ \\ 3=a(0+1)^2+2 \\ 3=a*1^2+2 \\ 3-2=a \\ a=1 \end{gathered}`

Then, in vertex form the function of the blue parabola is:

`y=(x+1)^2+2`

Remove parentheses to find it in standard form:

`\begin{gathered} y=(x^2+2x+1^2)+2 \\ y=x^2+2x+3 \end{gathered}`

___________

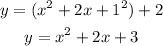
Red parabola:

Vertex (0,3)

`\begin{gathered} y=a(x-0)^2+3 \\ y=ax^2+3 \end{gathered}`

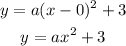
Use a point to find a:

`\begin{gathered} (-1,2) \\ 2=a(-1)^2+3 \\ 2=a+3 \\ 2-3=a \\ a=-1 \end{gathered}`

Equation in vertex form:

`y=-x^2+3`

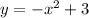
Then, the functions in the given graph are:

`\begin{gathered} f(x)=x^2+2x+3 \\ g(x)=-x^2+3 \end{gathered}`