We have the expression:
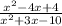
We have to factorize both numerator and denominator:
![\begin{gathered} \text{For }x^2-4x+4\colon \\ x=\frac{-(-4)\pm\sqrt[]{(-4)^2-4\cdot1\cdot4}}{2\cdot1} \\ x=\frac{4\pm\sqrt[]{16-16}}{2} \\ x=(4\pm0)/(2) \\ x=2 \\ \longrightarrow x^2-4x+4=(x-2)^2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/h55dfghyrpjoqopcb1bhrc6shhnx03l5xn.png)
![\begin{gathered} \text{For }x^2+3x-10\colon \\ x=\frac{-3\pm\sqrt[]{3^2-4\cdot1\cdot(-10)}}{2\cdot1} \\ x=\frac{-3\pm\sqrt[]{9+40}}{2} \\ x=\frac{-3\pm\sqrt[]{49}}{2} \\ x=(-3\pm7)/(2) \\ x_1=(-3-7)/(2)=-(10)/(2)=-5 \\ x_2=(-3+7)/(2)=(4)/(2)=2 \\ \to x^2+3x-10=(x+5)(x-2) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9uvdnhcdkwzss4968epy1ecg2kdmd5xb5h.png)
As we have a common factor, we can simplify the expression as:
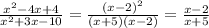
The restricted values for x are the ones that make the expression become undefined. This happens when, for example, the denominator becomes 0.
In this case, when x=-5, the denominator x+5=-5+5=0 and the expression is undefined.
This is the only restricted value for this expression.
Answer:
The reduced expression is (x-2)/(x+5).
The restricted value is x=-5.