Question

F(x)=X^2-6x+9 show final answer as the product of two bionomials

Answer 1

`f(x)=(x-3)(x-3)`

Step-by-step explanation

Step 1

`f(x)=x^2-6x+9`

we have a trinomial in the form

`x^2+bx+c`

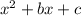
To factor a trinomial in the form x^2 + bx + c, find two integers, r and s, whose product is c and whose sum is b. Rewrite the trinomial as x^2 + rx + sx + c and then use grouping and the distributive property to factor the polynomial. The resulting factors will be (x + r) and (x + s)

`\begin{gathered} s+r=-6 \\ s\cdot r=9 \\ so \\ s=-3 \\ r=-3 \end{gathered}`

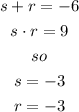
Step 2

now , to write the trinomial in the form x^2 + bx + c as the prodcut of two binomials, use(after you get r and s)

factor 1:( x+r)

factor2(x+s)

`\begin{gathered} x^2+bx+c=(x+r)(x+s) \\ so \\ f(x)=x^2-6x+9 \\ f(x)=(x-3)(x-3) \end{gathered}`

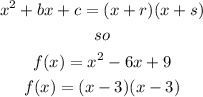
I hope thi helps you